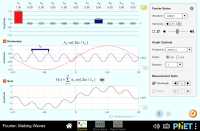
Fourier: Creando Ondas

Paquete de recursos:

Descripción:

Suma senos o cosenos para crear ondas de diferentes formas. Descubre cómo al cambiar las amplitudes de los distintos armónicos cambia el sonido que escuchas. Juega al juego de las ondas y combina los armónicos para que coincidan con una forma de onda especifica. Construye paquetes de ondas y explora los efectos de cambiar el espacio entre los componentes de Fourier y la anchura del paquete de ondas.

Objetivos de aprendizaje:
1. Explicar cualitativamente cómo los senos y cosenos se suman para producir funciones periódicas arbitrarias.
2. Reconocer que cada componente de Fourier corresponde a una onda sinusoidal con una longitud de onda o período diferente.
3. Describir los sonidos en términos de ondas sinusoidales.
4. Comparar y contrastar las ondas en el espacio y las ondas en el tiempo.
5. Reconocer que la longitud de onda y el periodo no corresponden a puntos específicos de la gráfica, sino que indican la longitud/tiempo entre dos valles consecutivos, picos o cualquier otro punto correspondiente.
6. Relacionar la notación matemática de una serie de Fourier con su representación gráfica y determinar qué aspecto de la gráfica describe cada uno de los símbolos de la ecuación.
7. Reconocer que λ & T y k & ω son análogos, pero no iguales.
8. Traducir una ecuación de la notación sumatoria a la notación expandida.
9. Reconocer que la anchura de un paquete de ondas en el espacio de posición está inversamente relacionada con la anchura de un paquete de ondas en el espacio de Fourier.
10. Explicar cómo el Principio de Incertidumbre de Heisenberg resulta de las propiedades de las ondas.
11. Reconocer que el espaciado entre las componentes de Fourier está inversamente relacionado con el espaciado entre los paquetes de ondas, y que una distribución continua de las componentes de Fourier conduce a un único paquete de ondas.

Recursos relacionados:

Tipo de recurso educativo:

Simulación

Autor:

Elaboración de diseño: Amy Rouinfar, Sam McKagan
Desarrollo de software: Chris Malley (PixelZoom, Inc.)
Equipo: Wendy Adams, Mike Dubson, Danielle Harlow, Ariel Paul, Kathy Perkins, Carl Wieman
Análisis de calidad: Logan Bray, Clifford Hardin, Brooklyn Lash, Emily Miller, Nancy Salpepi, Kathryn Woessner

Titular de los derechos:

PhET™ Interactive Simulations
© University of Colorado Boulder 2002-2024