28 ¿Cree que Ana es demasiado pequeña para su edad? La distribución normal.

Diapositiva 0

Un maravilloso día para todos. Bienvenidos a este nuevo episodio, en el que hablamos -como siempre- de matemáticas. Esta vez también se trata de una distribución de probabilidad. Se trata de la distribución normal, una distribución importante con muchas aplicaciones interesantes.

Diapositiva 1

Partimos de esta pregunta en general:

¿Con qué probabilidad toma una variable aleatoria determinados valores?

Consideremos primero lo que ya sabemos en este contexto.

Un ejemplo sencillo es, como suele ocurrir, el de los dados normales de seis caras. Cada uno de los resultados 1, 2, 3, 4, 5 y 6 ocurre con la misma probabilidad de p = 1/6. Esto puede verse como una distribución uniforme.

En el último episodio también estudiamos la distribución binomial y llegamos a entenderla con una fórmula. ¿Quizás esto también funcione con otras distribuciones de probabilidad? Sí, ciertamente es posible. Y de eso es de lo que hablamos hoy.

Diapositiva 2

Hay, por supuesto, diferentes distribuciones de probabilidad (con nombre y sin nombre) que ciertamente no podemos ni mirar ni describir fórmulas. Por lo tanto, a continuación, veremos sólo un ejemplo más, pero muy importante. Es la distribución normal y se refiere -al igual que la distribución binomial- a toda una clase de experimentos aleatorios.

De esto se trata:

¿Es Ana un poco pequeña para su edad?

Diapositiva 3

Veamos primero esta distribución de probabilidad de forma cualitativa. Está presente en muchos contextos cotidianos.

Por ejemplo

• Altura
• Peso
• Perímetro cefálico

se distribuyen de manera normal en los recién nacidos.

¿Qué significa eso? Cualitativamente, es sencillo: hay un valor medio y alrededor de este valor medio los valores medidos se encuentran relativamente más cerca con mayor probabilidad que más lejos.

Diapositiva 4

Fijémonos en la altura de los niños. La OMS, la Organización Mundial de la Salud, publicó en 2006 datos sobre esta y otras características, recogidos en seis países: Brasil, Ghana, India, Noruega, Omán y Estados Unidos.

En la publicación correspondiente, por ejemplo, hay información sobre la altura de las niñas recién nacidas en la tabla 27 de la página 64. Veamos con más detalle esta tabla.

Diapositiva 5

Este es un extracto de la tabla:

El valor medio de la altura de las niñas al nacer es de 49,1 cm, la desviación estándar es de SD = 1,9 cm. También se indican los percentiles

¿Recuerda lo que son los percentiles? Son los números de la fila superior de la tabla e indican porcentajes. Por ejemplo, "75" significa que el 75% de las niñas recién nacidas no superan el valor correspondiente de 50,4 cm.

Entraremos en más detalles en la siguiente diapositiva.

Hay que destacar que el valor medio aquí es la mediana. Denota - y lo hemos usado más a menudo - la marca del 50%.

Diapositiva 6

Entonces, ¿de qué se tratan los percentiles?

Supongamos que Ana, que acaba de nacer, mide 46 cm. Entonces estaría en el 5% inferior de los bebés femeninos en términos de altura.

Si se miden 48 cm, entonces pertenecería al 25% inferior de los bebés femeninos en términos de altura. Sin embargo, este valor seguiría estando dentro de una desviación estándar, que se cifró en 1,9 cm.

Supongamos que Ana mide 49 cm. Entonces, estaría en medio de los bebés femeninos en términos de altura y aproximadamente la mitad serían más altos o más bajos que ella.

¿Y 54 cm? Eso sería bastante grande, porque el 99% de los bebés femeninos nacen más pequeños que Ana.

Diapositiva 7

A partir de esto, se pueden determinar las desviaciones de la altura media. La simetría es sorprendente.

Diapositiva 8

Y lo ponemos en un diagrama. Las barras rojas muestran los valores absolutos de los percentiles. Las barras azules, en cambio, pretenden ilustrar la desviación de la mediana y, por tanto, el valor esperado. Las desviaciones hacia arriba y hacia abajo se muestran de la misma manera.

Y es esta desviación la que está en cuestión. Desde luego, no es de extrañar que muestren una cierta simetría y que las desviaciones hacia arriba y hacia abajo sean bastante similares a aproximadamente la misma distancia de la mediana.

Se puede ver (con un poco de imaginación si es necesario) la curva de campana de Gauss.

Diapositiva 9

Volvamos a ver las lecturas.

La desviación estándar está dada por la OCDE como 1,8627 cm con cuatro decimales.

Si se tiene en cuenta una desviación estándar (o más), el rango es de hasta 47,3 cm o de 51,0 cm de altura.

Si se tienen en cuenta dos desviaciones estándar (o más), el rango es de hasta 45,4 cm o de 52,9 cm de altura.

Una desviación estándar o más se mide en consecuencia para menos del 25% superior o inferior de las niñas recién nacidas. Dos desviaciones estándar es mucho y menos que el 3% superior o inferior de las niñas recién nacidas también entran en este rango.

Diapositiva 10

Y eso caracteriza a la distribución normal.

Con una distribución normal, el 68,3% de los datos se encuentran en un rango determinado por el valor esperado +/- 1 desviación estándar.

Así, en el ejemplo, el 68,3% de los recién nacidos tienen una altura entre 47,3 cm y 51,0 cm.

Con una distribución normal, aproximadamente el 95,5% de los datos se encuentran en un rango determinado por el valor esperado +/- 2 desviaciones estándar.

En el ejemplo, alrededor del 95,5% de los recién nacidos tienen una altura entre 45,4 cm y 52,9 cm.

Diapositiva 11

Pero, por supuesto, también queremos analizar la cuestión de forma más sistemática.

Si se hace esto, se pasa de la distribución binomial a la distribución normal. Para muestras grandes, los histogramas de las variables aleatorias con distribución binomial pueden aproximarse mediante curvas de campana. ¿Se acuerda? Lo vimos en el último episodio en un histograma cuando lanzamos un dado 50 veces con los resultados "6" o "no 6".

Realmente funciona mejor a través de simulaciones adecuadas. Las curvas de campana se pueden aproximar mediante el término

Aquí μ denota el valor esperado y σ la desviación estándar.

Diapositiva 12

Lo definimos.

Si una variable aleatoria con valor esperado m y desviación estándar σ puede ser descrita por la función

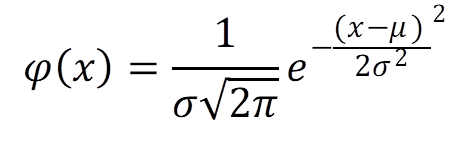
-       la “densidad de probabilidad“ - entonces se denomina de distribución normal.

Una variable aleatoria se llama distribución normal estándar, si el valor esperado m = 0 y la desviación estándar σ = 1. Lo que se obtiene entonces es la curva de campana de Gauss.

Diapositiva 13

Muchas cosas de nuestra vida cotidiana tienen una distribución normal o aproximadamente normal. Por lo tanto, se puede - y por supuesto con una gran muestra - asumir una distribución normal en estos casos:

Altura y peso incluso en adultos; rendimiento de los alumnos en el salto de altura o de longitud; peso de las bolas de helado, paquetes de té, barras de pan, etc.; número de ositos de goma en una bolsa de 100 g.

En todos estos casos, existe un valor medio por debajo o por encima del cual se encuentra el 50% de los valores medidos, y alrededor del cual la mayoría de los valores medidos se situarán en una distancia bastante pequeña. Y habrá desviaciones tanto al alza como a la baja.

Diapositiva 14

Gracias por acompañarme hoy. Nos volveremos a encontrar en el próximo episodio y hablaremos, cómo no, de matemáticas.