Una vez determinado, ¿siempre es válido? La probabilidad y el problema de la cabra.
24 Una vez determinado, ¿siempre es válido? La probabilidad y el problema de la cabra.
Diapositiva 0
Bienvenidas y bienvenidos a este nuevo episodio. Una vez más estamos hablando de matemáticas. Se trata de una cabra y de un problema que puede causar. Bueno, y también sobre la probabilidad condicional.
Diapositiva 1
Experimentos aleatorios de varias etapas y probabilidades condicionales: ya lo tratamos en el episodio anterior. No se complicó tanto, nos limitamos a experimentos aleatorios de dos etapas. Pero, por supuesto, también puede ser más complejo, y sólo un poco más complicado.
Diapositiva 2
Comenzamos con un caso muy sencillo que también puede llevarse a cabo de forma práctica. Lanzamos una moneda tres veces y miramos la probabilidad de que salga “sello” exactamente dos veces
Esto es realmente claro desde un punto de vista matemático.
Es P(cara) = P(sello) = 1/2. En consecuencia, la probabilidad para una secuencia dada de caras y sellos es 1/2 x 1/2 x 1/2 = ½3 = 1/8 .
Hay ocho posibilidades en total. ¿Cuántas de estas son "favorables"?
Diapositiva 3
Un diagrama de árbol es una buena opción en este caso, porque se puede, al menos en teoría, representar cualquier número de niveles. Y también podemos ver fácilmente el resultado. De los ocho casos posibles, hay tres en los que el sello está dos veces arriba. Aquí están marcados con un punto verde.
Diapositiva 4
Ahora bien, a veces hay que tener en cuenta las condiciones, y también veremos un ejemplo de ello.
Ema es vecina de Ana y Carlos. Su gata ha tenido cuatro gatitos.
Carlos sabe que hay un macho entre ellos. Ana le dice que incluso ha visto dos gatitos machos. ¿Podría haber también crías hembras? Ambos lo piensan, y de momento por separado.
Diapositiva 5
Carlos refleja que en principio hay cinco posibilidades: No hay gatito macho o hay uno o dos o tres o cuatro. Sin embargo, según su información, una de estas posibilidades está descartada, porque sabe que al menos uno de los gatitos es macho. Eso deja cuatro posibilidades en las que hay al menos un varón. En una de estas posibilidades, todos los animales son machos. Así que hay tres casos favorables y, por tanto, una probabilidad de 3/4 para al menos una gatita.
Ana tiene más información, y por eso puede excluir dos de las cinco posibilidades. De las tres posibilidades restantes, dos son favorables: llega a la probabilidad (más baja) de 2/3 para una gatita.
Diapositiva 6
Sí, obviamente la evaluación de la probabilidad de un evento no es necesariamente fija. Más bien, puede depender de diferentes informaciones. Y precisamente en eso consiste el problema de la cabra.
Diapositiva 7
Imagine que le permiten salir en la televisión. En un espectáculo, el premio principal, un hermoso coche, le llama la atención y sólo una pregunta le separa de él. Sin embargo, se necesita un poco de suerte para responder a esta pregunta. Pero los conocimientos matemáticos tampoco están de más.
Diapositiva 8
Esta es la situación.
Se encuentra frente a tres puertas cerradas. Detrás de una de estas hay un hermoso y flamante coche, detrás de las otras dos hay cabras. Puede elegir una puerta y confiar en su suerte.
Supongamos que elige la primera puerta. Ahora el moderador -y el conoce la solución del acertijo- no abre esta puerta, sino la tercera. Detrás de ella hay una cabra. Le pregunta si quiere seguir con su elección original o si prefiere que se abra la segunda puerta.
¿Qué le parece? ¿Importa cuál de las dos puertas elija? ¿O hay más posibilidades de ganar con una de las dos puertas?
¡Da un tip!
Diapositiva 9
Analizamos la situación en detalle, como solemos hacer.
En el primer paso se elige arbitrariamente una puerta, la probabilidad de ganar es entonces, obviamente, de 1/3. Hay un caso favorable entre tres posibles.
Diapositiva 10
En el segundo paso, el moderador abre la tercera puerta.
La tensión va en aumento. ¿Qué hay detrás?
Diapositiva 11
Hay una cabra detrás de la puerta 3, por lo que el coche se puede encontrar en un lugar diferente. Supongamos que ha elegido la puerta 1 y que está considerando la conveniencia de un cambio. Todavía existen (claramente) estas tres posibilidades:
La ganancia está detrás de la puerta 1 o
La ganancia está detrás de la puerta 2 o
La ganancia está detrás de la puerta 3.
Diapositiva 12
Vamos a jugar con las situaciones.
La ganancia está detrás de la puerta 1. Entonces, simplemente no tiene suerte si se cambia.
La ganancia está detrás de la puerta 2. Entonces el moderador no puede abrir la puerta 1 porque usted lo sugirió y la puerta 2 porque ahí está el premio. Abre la puerta 3, un cambio a la puerta 2 es favorable para usted.
La ganancia está detrás de la puerta 3. Entonces el moderador no puede abrir la puerta 1 porque usted lo sugirió y la puerta 3 porque ahí está su ganancia. Abre la puerta 2, un cambio a la puerta 3 es favorable para usted.
En otras palabras: En dos de cada tres situaciones, el cambio le es favorable y su probabilidad de ganar aumenta a 2/3.
Diapositiva 13
Y ahora de forma bastante sistemática. Se trata de estos eventos:
Gi := La ganancia está detrás de la puerta i (para i = 1,2,3).
Mi := El moderador abre la puerta i (para i = 1,2,3).
Al principio, todo es bastante sencillo para usted y no requiere mucha reflexión.
No tiene información y por eso P(G1) = P(G2) = P(G3) = 1/3.
Diapositiva 14
Ahora ha elegido la puerta 1 y suponemos que el moderador ha abierto la puerta 3.
Entonces buscamos P(G1|M3) y P(G2|M3).
Ahora bien, esto requiere un trabajo de antemano. Consideramos la probabilidad de que el moderador abra la puerta 2 o la puerta 3. Y por supuesto, tenemos en cuenta que eligió la puerta 1.
Diapositiva 15
Eligió la puerta 1, el moderador abrió la puerta 3. Acabamos de ver las posibilidades en este caso. Vamos a preguntarles de nuevo.
¿Por qué es P(M3|G1) = 1/2?
Usted dice "puerta 1", que también sería la ganancia en este caso. El moderador puede elegir libremente entre las puertas 2 y 3 al abrir, por lo que la probabilidad de que elija la puerta 3 es 1/2.
¿Por qué es P(M3|G2) = 1?
Usted dice "puerta 1", hay una cabra detrás de ella. El moderador no puede abrir la puerta 1 (su elección) y tampoco la puerta 2 (¡¡¡Gana!!!). Elige la puerta 3 con seguridad.
¿Por qué es P(M3|G3) = 0?
Bueno, eso iría realmente en contra del espíritu del juego.
Diapositiva 16
Tomamos -y este es un detalle importante- el punto de vista del moderador. Este es el resumen, usted ya conoce los números.
Diapositiva 17
¿Recuerda la fórmula de Bayes?
Hay una extensión que ahora también permite una solución formal del problema (y la justificación se puede encontrar en la literatura pertinente). Se necesita
![]()
![]()
![]()
![]() P(M3|G2) = 1 P(M3|G3) = 0
P(M3|G2) = 1 P(M3|G3) = 0
Y se calcula
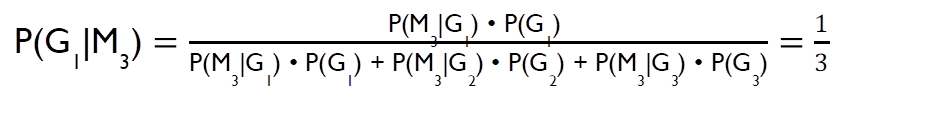
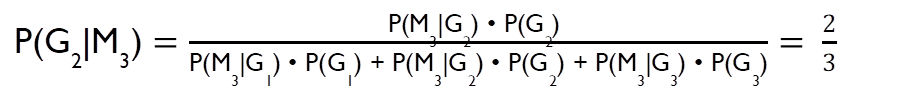
Dicho de otro modo. La probabilidad de la puerta 1 era antes un tercio y no cambia. La información adicional aumenta la probabilidad de la puerta 2.
Diapositiva 18
¿Qué hicimos hoy?
De alguna manera, volvimos a aprender algo sobre nuestra escasa intuición para las correlaciones en estadística y probabilidad. Pero eso no fue todo. Hemos visto que la perspectiva juega un papel importante.
- En el problema de la cabra, es fundamental para la evaluación que el moderador conozca la solución correcta.
- En el caso de los gatitos, también fue la información concreta la que influyó en la determinación de las probabilidades.
Conclusión: no se trata en primer lugar de fórmulas y cálculos, sino de la interpretación de una situación sobre estadística y probabilidad.
Diapositiva 19
Gracias por acompañarme, hoy no ha sido fácil. Tal vez le reconforte saber que hace tiempo hubo acaloradas discusiones sobre el problema de la cabra y su correcta solución, y que los matemáticos también se equivocaron al respecto. Hasta la próxima vez, espero verle.