26 El casino siempre gana: variables aleatorias.

Diapositiva 0

Los inicios de la teoría de la probabilidad estuvieron fuertemente influenciados por los juegos de azar, que en principio no dieron la mejor reputación a esta rama de las matemáticas. En consecuencia, en estos episodios sobre la probabilidad intentamos repetidamente llamar la atención sobre otras aplicaciones, normalmente más interesantes.

Hoy hay una excepción. Con el nuevo tema de las variables aleatorias, realmente tiene sentido pensar en por qué muchas personas han perdido dinero apostando, pero rara vez se informa sobre el colapso de un casino, si es que alguna vez lo hace.

Diapositiva 1

Las variables aleatorias -acabamos de utilizar el término- son simplemente funciones.

Pero, ¿qué es exactamente una variable aleatoria? ¿Qué hay detrás de este nuevo tipo de funciones? Vamos a resolverlo paso a paso. Una vez más, se trata de observar y clasificar las situaciones en las que interviene el azar.

Diapositiva 2

Ya he dicho que el juego jugará un papel importante hoy. ¿Conoce el juego "Chuck-a-luck"? El nombre significa más o menos “amigo de la suerte”. Vamos a ver si es un verdadero amigo.

Las reglas son muy sencillas.

Apuesta 1 euro y juega contra la banca. Se elige un número entre el 1 y el 6. Luego se lanzan tres dados.

Si al menos un dado muestra el número que eligió, recupera su apuesta y 1 euro adicional por cada dado con el número elegido.

Si su número no aparece, la apuesta se pierde.

Diapositiva 3

La pregunta central para usted: ¿Qué cambia en su cartera?

Esto puede describirse mediante una función. Se puede asignar únicamente un número del conjunto {-1; 1; 2; 3} a cada resultado del experimento aleatorio "lanzamiento triple de dados", porque o se pierde un euro, o se ganan 1 o 2 o 3 euros.

Supongamos, que eligió el „6“.

Entonces se ve así: Falta un euro en la cartera para todas las combinaciones de tres sin un 6. Y hay tres euros más sólo para el triple (6,6,6).

Diapositiva 4

Generalmente, a cada triple de tres números (y estos son los lanzamientos) se le asigna una ganancia o una pérdida. Esta función tiene el dominio y el codominio Ω = { -1, 1, 2, 3 } .

A los 6³ = 216 triples de números enteros entre el 1 y el 6 se les asigna uno de los números de Ω.

Diapositiva 5

Vamos a reproducirlo concretamente.

Supongamos que el jugador elige "6". Para todas las combinaciones de tres sin 6, falta un euro en la cartera. Son todas las combinaciones de tres números entre el 1 y el 5.

Puede ver estas posibilidades aquí.

Una vez más, en sólo uno de los 216 casos se ganan tres euros.

Diapositiva 6

Necesitamos una definición para el nuevo concepto.

Sea W un espacio de resultados finito. Entonces cualquier función X desde el conjunto Ω hacia el conjunto de los números reales (y sí, en realidad la mayoría de las veces va hacia un subconjunto significativo) se llama una variable aleatoria de Ω. Por lo tanto, se asigna únicamente un número real X(ω)  a cada ω de Ω.

Si se asigna a cada valor posible de la variable aleatoria la probabilidad con la que asume ese valor, se obtiene la distribución de probabilidad de la variable aleatoria.

Teniendo en cuenta estos términos, veamos de nuevo el ejemplo.

Diapositiva 7

En el ejemplo de chuck-a-luck el dominio de la variable aleatoria es

 

y el codominio es W  =  {-1, 1, 2, 3} .

¿Y qué pasa con las probabilidades de los resultados individuales y, en consecuencia, con la distribución de probabilidades?

Diapositiva 8

Por lo tanto, nos interesan los valores de

          P(X = -1)

          P(X =  1)

          P(X =  2)

          P(X =  3)

Esto puede servir para determinar si esta apuesta vale la pena para los jugadores.

Diapositiva 9

Es fácil determinar las probabilidades, las reglas de la combinatoria ayudan aquí. Se trata simplemente de determinar los casos favorables y los posibles. Hay un total de 6³ = 216 posibilidades de combinaciones de tres. De ellos, 5³ = 125 no contienen un "6". Si se lanza un "6" una vez y otro número dos veces, entonces hay 3 x 5² = 75 posibilidades para ello, porque los otros números pueden ser lanzados en primer y segundo lugar, primero y tercero o segundo y tercero. Si lanza un "6" dos veces, una vez otro número, entonces hay 3 x 5 = 15 posibilidades. El otro número puede ser lanzado en primer, segundo o tercer lugar. Y por último, la combinación de tres veces "6" ocurre exactamente una vez.

En consecuencia

Diapositiva 10

Si se utiliza una tabla para la representación, se puede ver la distribución de la probabilidad de un vistazo. La primera línea muestra las posibles ganancias y la segunda las probabilidades correspondientes.

Diapositiva 11

Ahora se puede trabajar con estos números y pensar en lo que ocurre cuando se juega de forma persistente. Si lo hace, a la larga se pierde 1 Euro en 125 de 216 casos.

Se gana 1 Euro en 75, 2 Euros en 15 y 3 Euros en 1 de 216 casos.

Con estos valores, se podría "ponderar" y así determinar una "media de ganancias" (o media de pérdidas, según el caso) por partido.

Diapositiva 12

Puede verlo aquí. Multiplicamos la pérdida de 1 euro o – mejor – las posibles ganancias por la respectiva probabilidad y formamos la suma. El resultado es - 17/216 o aproximadamente 0,08. Lo llamamos "valor esperado".

No es difícil ver que, aunque haya una pequeña pérdida, sigue habiendo una pérdida por parte del jugador. Y esta pérdida es de 8 céntimos por partido de media.

Diapositiva 13

El valor esperado de una variable aleatoria es la suma de la probabilidad de cada posible suceso aleatorio multiplicado por el valor de dicho suceso:

El valor esperado es, por tanto, (como ya se ha mencionado) el valor medio de la variable aleatoria por ensayo a largo plazo.

Diapositiva 14

Una vez más en concreto:

¿Es el juego chuck-a-luck un juego justo? Obviamente, en un juego justo debería ser E(X) = 0. Lo hemos calculado, E(X) < 0.

Así que, con una repetición muy frecuente, se puede esperar una pérdida media de unos 8 céntimos por partida y eso significa que no es un juego justo – aunque no es sorprendente.

Diapositiva 15

El valor esperado y los cálculos necesarios en este caso se pueden ilustrar muy bien, al menos en este caso con un dominio pequeño.

Imagina una barra etiquetada como una línea numérica. En los puntos -1, 1, 2 y 3 hay cuerpos con las masas 125/216, 75/216, 15/216 y 1/216. Entonces se puede definir el valor esperado como el "centro de gravedad". Si uno apoya la viga aquí, entonces la viga está en equilibrio.

Diapositiva 16

Veamos otro ejemplo. Nos quedamos en el contexto del azar.

¿Ha jugado alguna vez a la ruleta?

Una bola rueda y encuentra (al menos en la variante europea) uno de los 37 números, de los cuales 18 tienen fondo rojo, 18 tienen fondo negro y uno tiene fondo verde. Una forma sencilla de apostar: se apuesta al ROJO o al NEGRO. Si la apuesta de color sale, las ganancias son el doble de la apuesta. De lo contrario, se pierde la apuesta.

Suena bien, ¿verdad? ¿Un juego justo? Haga las cuentas. Vuelva a apostar 1 euro.

Diapositiva 17

¿Un juego justo? No en absoluto, se puede descartar inmediatamente.

De las 39 posibilidades, sólo 18 – y por tanto menos de la mitad – son casos favorables. Esto sólo puede acabar bien para el casino.

No obstante, calculamos: En 18 de los 37 casos se gana 1 Euro, en 19 de los 37 se pierde 1 Euro.  Así es:

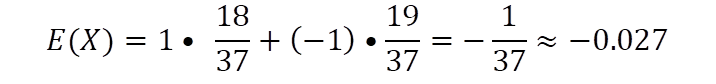
Diapositiva 18

Por favor, abra un casino. El sólido conocimiento de las matemáticas también debería dar sus frutos financieros algún día.

Ofrece este juego en el que la apuesta vuelve a ser de 1 euro:  se lanzan dos dados. La apuesta se pierde si no se lanza un "6".  ¿Cómo podrían ser las ganancias con uno o dos "6" para no acabar en números rojos y que el juego no sea demasiado injusto?

Diapositiva 19

El valor "-1" es evidente, no puede dejar que sus clientes pierdan más que la apuesta. Lo que se busca son las ganancias m y n cuando se lanza un "6" una o dos veces.

Buscamos soluciones a la inecuación

           

Obviamente, con ≥ 0 nuestra existencia estaría en peligro.

Si se le da una nueva forma, parece más simple. Buscamos soluciones a la inequidad   n + 10•m < 25 .

En principio, hay un número infinito de soluciones a una inecuación con dos incógnitas. Lo analizaremos más detenidamente dentro de un momento.

Diapositiva 20

Aquí hay ejemplos de soluciones.

Para n = 2  y  m = 1 se calcula  2 + 10•1 = 12 < 25

Para n = 2  y  m = 1,5 se calcula  2 + 10•1,5 = 17 < 25

Para n = 4  y  m = 2 se calcula  4 + 10•2 = 24 < 25

Por lo tanto, estas ganancias son elegibles para su casino. Pero se puede dudar de que sus clientes estén satisfechos con una ganancia demasiado pequeña como la de la primera o segunda línea.

Diapositiva 21

Ya se nota. No es tan fácil mantener el equilibrio adecuado. Sin embargo, el valor esperado permite una buena evaluación de la situación.

Diapositiva 22

Eso es todo por hoy. Todo lo mejor para usted y me alegro de que haya estado allí. Hasta la próxima.