25 La parte más difícil de la combinatoria. Una distribución completamente injusta de manzanas a los niños.

Diapositiva 0

Bienvenidos y bienvenidas a un nuevo episodio. Hoy volvemos a hablar de combinatoria y a resolver un problema que íbamos postergando. Repartimos manzanas a los niños y dejamos de lado toda la imparcialidad.

Diapositiva 1

¿Se acuerda al modelo de urna?

Ya tratamos esto en los primeros episodios y sacamos bolas de una urna. Era importante distinguir entre sacar con y sin devolver la bola; también se puede decir con y sin repetición; y con y sin prestar atención a la secuencia.

Combinando estas formas de sacar, hay cuatro maneras diferentes de hacerlo. Sin embargo, hasta ahora sólo tratamos tres casos.

Veamos brevemente cuáles eran y repitamos al menos las fórmulas correspondientes.

Diapositiva 2

Este fue el primer caso que examinamos: Sacar con repetición y prestando atención a la secuencia.

Veamos un ejemplo. En esta urna hay ocho bolas de diferentes colores. Así que hay ocho posibilidades de sacar una de estas bolas. Si se hace esto varias veces seguidas y se devuelve la bola cada vez, entonces también se tienen estas ocho posibilidades con cada nuevo movimiento.

Si se saca una bola cinco veces, obtendrá

8 • 8 • 8 • 8 • 8 = 8⁵ =  32.768

posibilidades.

Eso es sacar con repetición y con prestar atención a la secuencia.

O – en otras palabras – sacar con devolver y cuidando el orden.

Diapositiva 3

En general: De un conjunto con n elementos se puede obtener

n • n • n • … • n = n^k  k-tuplas.

También habíamos llamado a esto palabras de k caracteres.

Diapositiva 4

En otro caso, se trataba de sacar sin repetición, pero se continúa cuidando el orden.

Primero puede elegir entre ocho bolas. En el siguiente paso, por supuesto, falta la bola sacada, de modo que sólo tiene siete para elegir. Si saca cinco veces seguidas, tiene 8 x 7 x 6 x 5 x 4 posibilidades. Y esto también se puede escribir como  

Diapositiva 5

Así es como se ve en general:

De un conjunto con n elementos se puede obtener  ordenamientos de k elementos. Estos ordenamientos se denominan k-permutaciones.

Diapositiva 6

Y ese fue el tercer caso que analizamos. Volvemos a sacar sin repetición y no nos interesa el orden.

Ya conoce este ejemplo. A Pati le gusta viajar, tiene cinco vestidos. ¿Cuántas posibilidades tiene de meter tres en su maleta?

De nuevo, hay cinco posibilidades para el primer vestido, otras cuatro para el segundo y, finalmente, tres para el tercero.

Diapositiva 7

Entonces, ¿5 x 4 x 3 es la solución? Claro qué no. No importa si saca primero el vestido rojo del armario y luego el verde, o si los saca en orden inverso. Por lo tanto, se trata de contar todas las mismas combinaciones de vestidos una sola vez.

Diapositiva 8

Y eso significa dividir por 3! para tres vestidos. En este caso hay

 

posibilidades diferentes.

Diapositiva 9

Otra vez en general: Al sacar sin devolver y sin atender al orden, se trata del número de subconjuntos con k elementos de un conjunto con n elementos. Esto es .

Diapositiva 10

Evidentemente, falta el caso en el que sacamos una bola de una urna, la volvemos y no nos interesa el orden.

He aquí un ejemplo: Repartimos 8 manzanas entre 5 niños. ¿Cuántas distribuciones diferentes son posibles? Al hacerlo, aceptamos conscientemente duras injusticias. Puede ocurrir que un niño no reciba una manzana o que reciba varias manzanas a la vez.

Tómese un momento y piense por qué este ejemplo es adecuado. ¿Quién o qué se está sacando en realidad aquí?

Diapositiva 11

No. No ponemos niños en una urna, por supuesto.

Pero qué tal cinco bolas que etiquetamos con los números del 1 al 5. Cada número representa a un niño. Si se saca una bola, el niño correspondiente recibe una manzana.

Esto es entonces, obviamente, sacar con repetición y sin prestar atención a la orden.

El problema ahora es encontrar un modelo adecuado para esta situación con el fin de derivar de él el número de posibilidades (y una fórmula sensata).

Diapositiva 12

Utilicemos una tabla. Aquí se introducen tres posibles distribuciones a modo de ejemplo. En el primer caso, el niño 3 se va a casa con las manos vacías, en el segundo caso es el niño 5 y el niño 4 se lleva bastantes. Finalmente, en el tercer caso, el niño 5 se va a casa con las ocho manzanas. Como ya dije, aquí no nos interesa en absoluto la justicia.

Y, evidentemente, hay muchas otras posibilidades para esa distribución.

Diapositiva 13

Y ahora le pido que vea la situación de manera un poco diferente. Olvídese de los niños, olvídese de las manzanas, tome la tabla como algo abstracto.

Cada fila de la tabla puede entenderse como una secuencia de 5 + 8 - 1 caracteres, es decir, 8 cruces y 4 = 5 - 1 guiones.

Los guiones son los que separan los campos individuales de una línea entre sí. Y estos son, por supuesto, cinco campos - exactamente como la tarea los nombra. Por lo tanto, no escribimos 4 guiones, sino que elegimos la denominación 5-1.

Diapositiva 14

Una vez más: Cada fila de la tabla puede entenderse como una secuencia de 5 + 8 - 1 caracteres, es decir, 8 cruces y 4 = 5 - 1 guiones.

Así que estamos buscando los posibles lugares para 8 cruces.

Pero eso es exactamente lo que acabamos de tener.

Para la distribución de las 8 cruces a los lugares de 5 + 8 -1 caracteres, si el orden no importa y no se permiten repeticiones, hay exactamente

Posibilidades.

Diapositiva 15

Se puede calcular fácilmente y se obtiene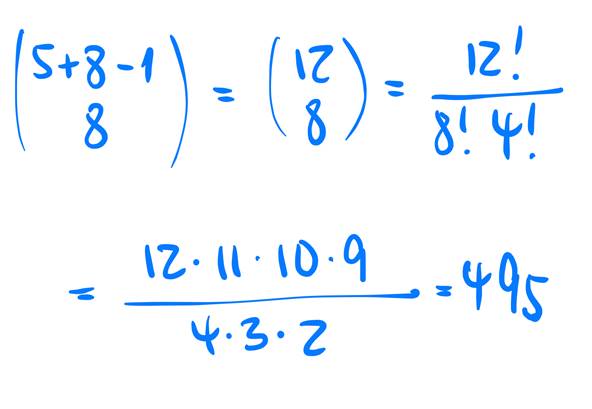

Diapositiva 16

En general, se ve así: Si seleccionamos k objetos de una urna con n objetos con repetición y sin prestar atención al orden, entonces hay para esto

posibilidades.

Diapositiva 17

No sé si le gustó el modelo. ¿Le apetece un segundo enfoque explicativo? Este es otro enfoque para resolver el problema.

De nuevo suponemos 8 manzanas A₁, A₂, … , A₈ y 5 niños K₁, … , K₅. Introducimos ambos como puntos en un diagrama.

Diapositiva 18

Se puede marcar por encima de los niños las manzanas que le tocan a cada uno. En este ejemplo, el primer y el tercer niño reciben dos manzanas cada uno, el cuarto una manzana y el quinto tres manzanas. El segundo niño no recibe nada. Si se consideran los niños y las manzanas, es decir, el eje x y el eje y, entonces cada asignación posible es un camino en este diagrama.

Diapositiva 19

Es un camino diferente, pero igual de largo. Bastante simple, en realidad. Hay 8 conexiones verticales, cada una de las cuales representa una manzana, y cuatro conexiones horizontales, los espacios entre los niños en el eje x.

Diapositiva 20

Este es otro de los caminos posibles. ¿Y cómo se procede sistemáticamente?

A continuación, buscamos todos los caminos de longitud 12 que constan de 8 tramos verticales y 4 horizontales.

Y obviamente es así: se eligen las secciones verticales, las horizontales son las fijas.

Esto nos devuelve a la idea básica de que "8 de 12" son elegidos.

Diapositiva 21

Así, en general, al sacar con repeticiones y sin tener en cuenta el orden, parece que tenemos que el número de k-combinaciones con repeticiones de un conjunto con n elementos es

 

Una k-combinación con repetición es otra expresión para una k-tupla o una serie k caracteres.

Diapositiva 22

En realidad, debería poder seleccionar primero las secciones horizontales para los trayectos de longitud 12, ¿no? Entonces, los tramos verticales serían fijos.

¿Puede funcionar? ¿No da eso un número completamente diferente?

No, eso funciona sin problemas. Lo sabemos:

Diapositiva 23

¿Quiere calcular usted mismo un ejemplo?

Sebastián tiene 6 pegatinas sonrientes idénticas. Quiere utilizarlas para colocarlas en 10 paquetes. ¿Cuántas posibilidades (posiblemente también completamente injustas) tiene?

Deténgase un momento, piense y calcule.

Diapositiva 24

Sebastián tiene 6 pegatinas sonrientes idénticas, entonces n = 6.

Quiere utilizarlas para colocar en 10 paquetes, entonces k = 10.

Se calcula así:

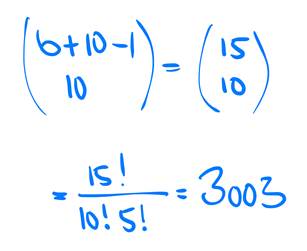
Diapositiva 25

Hacemos un resumen.

Existen cuatro posibilidades para seleccionar k elementos de un conjunto con n elementos. Puede sacar con o sin repetición, puede respetar el orden o no. Hemos elaborado una fórmula para cada uno de estos cuatro casos y puede verla aquí en la tabla.

Pero, por favor, no olvide que, sobre todo en clase, no puede tratarse de aplicar una fórmula. Realmente debería haberlo entendido de antemano.

Diapositiva 26

Gracias por estar ahí. Espero verle en el próximo episodio, en el que volveremos a hablar de matemáticas.