Diapositiva 0

Volvamos a charlar de matemáticas. Bienvenidos a este nuevo episodio. Hoy veremos algunos conceptos básicos de la estadística y veremos cómo se pueden integrar en una clase de matemáticas orientada a la acción. Vamos a analizar datos sencillos de una encuesta fácilmente realizable.

¡Empezamos!

Diapositiva 1

Imagínese que está planificando una encuesta en la escuela. Y, por supuesto, uno que una clase puede llevar a cabo y evaluar en su mayor parte por sí misma. El objetivo aquí es responder a esta pregunta, planteada inicialmente en términos muy generales:

¿Están los alumnos interesados en la asignatura de matemáticas? Nos gustaría comparar con la asignatura de español.

Diapositiva 2

¿Qué debería figurar el cuestionario? Por ejemplo, se podría preguntar por el nivel de estudios, la edad, el sexo, el interés por estas y otras asignaturas, la motivación para ocuparse del contenido de la asignatura respectiva en el tiempo libre, la asignatura favorita o las notas (por ejemplo, en el último examen).

Para cada pregunta, es importante aclarar previamente dos aspectos esenciales.

En primer lugar, hay que estar seguro de por qué se hace una determinada pregunta. Este aspecto no sólo es una propedéutica para el trabajo guiado por hipótesis, sino que también da la oportunidad de abordar el tratamiento de los datos en relación con la protección de los mismos.

En segundo lugar, hay que pensar en el cómo. ¿Recoge la edad en años o en años y meses? ¿Qué nivel de sofisticación se puede emplear de forma útil? Por ejemplo, ¿el interés por un tema se asigna en una escala de cuatro o cinco puntos? Por supuesto, el cómo está estrechamente ligado al por qué. 

Diapositiva 3

Los datos que se recogen aquí son muy diversos. Los datos como el sexo o la asignatura favorita se denominan datos cualitativos. Una codificación de ellos está basada en características cualitativas. Sencillamente -y esto se permite en muchas situaciones en el aula- se trata en su mayoría de datos con los que no se puede calcular de forma significativa.

Diapositiva 4

Datos como el nivel escolar, la edad o la nota del último examen son datos cuantitativos que se codifican con números. Así, se pueden ordenar y, por ejemplo, determinar la edad media de una muestra o calcular la nota media de los exámenes.

Pero cuidado, incluso estos valores deben interpretarse de forma significativa en el contexto de una encuesta. Una mejor nota en un examen se considera deseable, una mayor o menor edad no es necesariamente un signo de calidad y, sobre todo, no se puede evaluar fuera de un contexto específico.

Diapositiva 5

Y, por último, ¿qué hacemos con el interés por la asignatura o la motivación para abordar el contenido de la misma en el tiempo libre? También son datos cualitativos, si se toma un valor cualitativo de muy alto a muy bajo.

Diapositiva 6

Sin embargo, aquí es importante otra distinción, la que existe entre los datos ordinales y los nominales.

La edad, el nivel de estudios, las notas son ejemplos de datos ordinales, ya que se pueden ordenar de forma significativa. El sexo y la asignatura favorita son ejemplos de datos nominales, ya que no existe un orden coherente.

Sin embargo, también es posible ordenar datos como el interés y la motivación. Para ello, se codifica con números entre 1 y 5 en función del grado de expresión.

Hay que tener en cuenta que la alta motivación es aún más difícil de distinguir de la motivación media que, por ejemplo, una buena nota de una nota media en el colegio. Es importante saber que las distancias entre las expresiones individuales no son necesariamente las mismas.

Esas cifras se calculan, se determinan las medias y eso es perfectamente legítimo. Lo más importante es tener en cuenta los puntos débiles de una codificación a la hora de interpretar los datos.

Diapositiva 7

Vayamos a los términos. Partimos de la base de que todo el trabajo preliminar se ha completado y la encuesta se ha realizado.

882 alumnos de la Escuela Marie Curie de los cursos 5º a 10º rellenaron un cuestionario adecuado. Los resultados confirman la hipótesis: hay más alumnos que nombran el español como su asignatura favorita que los que nombran las matemáticas. Las otras asignaturas aterrizan -quizá de forma sorprendente- en el tercer puesto de la clasificación general.

En números absolutos, 441 estudiantes nombran el español como su asignatura favorita, para 312 son las matemáticas y para 129 otra asignatura. Es muy fácil obtener un importante concepto básico de estadística, a saber, la frecuencia absoluta. En cuanto a la pregunta sobre la asignatura favorita y la respuesta "matemáticas", la frecuencia absoluta es de 312.

Diapositiva 8

Ahora bien, 312 de 882 es ciertamente algo diferente a 312 de 1.000.000. ¿Qué podemos hacer con estos valores absolutos? Tiene sentido relacionarlos con la población. Por tanto, calculamos la frecuencia relativa como el cociente de la frecuencia absoluta y el tamaño de la población.

Y entonces tiene sentido pensar en una buena representación, que en este caso podría ser un gráfico circular, por ejemplo.

Los datos no han cambiado, pero son más fáciles de evaluar de esta manera. Exactamente la mitad de los alumnos nombró el español como su asignatura favorita, y un buen tercio dijo que las matemáticas. Y puede ver estos valores inmediatamente en el gráfico circular.

Diapositiva 9

Otra pregunta se refería al interés de los alumnos por las asignaturas de español y matemáticas. Se utilizó una escala de Likert que iba de 5 ("muy interesado") a 1 ("no interesado"). Una vez más, se miran primero los números absolutos, la lista original, y ya hemos utilizado este término antes.

Diapositiva 10

Pero también aquí la importancia de las frecuencias absolutas es limitada. Así que volvemos a buscar una representación adecuada que tenga sentido a simple vista. En este caso, podría ser un gráfico de barras.

Los valores pueden representarse muy bien uno al lado del otro, lo que facilita la comprensión de las diferencias, al menos cualitativamente. El español tiene valores máximos de interés alto y medio, las matemáticas también, pero la columna de interés alto es claramente inferior. 

Diapositiva 11

Con la debida precaución -ya lo hemos mencionado antes- determinamos una expresión media y calculamos la media aritmética. Para ello, simplemente ponderamos las expresiones individuales, es decir, los valores individuales de interés, y las dividimos por el tamaño de la muestra, es decir, el número de todos los estudiantes encuestados.

Un interés muy alto por las matemáticas fue marcado por 149 alumnos, por lo que este valor entra en el cálculo con 5 • 149. En total se obtienen ( 5 •149 + 4 • 206 + 3 • 256 + 2 • 174 + 1 • 97 ) : 882 y se redondean 3.15.

Diapositiva 12

Para la asignatura de español, el valor es de 3.48, por lo tanto -y como se esperaba de una primera mirada a los datos- más alto. Es una pena, porque también se han confirmado las expectativas que se tenían antes de la encuesta.

Por supuesto, cabe preguntarse si la diferencia entre los dos valores medios es realmente relevante o, por utilizar el término técnico, significativa.

Pospondremos la respuesta a un episodio posterior. Esto ya forma parte de "Estadística y probabilidad para profesionales" y, de todos modos, sólo se enseña en la escuela secundaria.

Diapositiva 13

Pero veamos qué más puede ser interesante a un nivel básico.

Volvemos a observar la serie de datos y descubrimos que más de la mitad de los alumnos tienen al menos un alto interés por el español como asignatura:

198 + 263 = 461 es mayor que 882 : 2 = 441.

Por cierto, la relación "mayor o igual que" sería suficiente para las siguientes consideraciones y por eso lo ve en la versión escrita.

La situación es diferente en el caso de las matemáticas, pero al menos más de la mitad de los alumnos tienen un nivel de interés medio. Es

149 + 206  + 256 = 611 , es mayor que 882 : 2 = 441

Pero

149 + 206  = 355 es menor que  882 : 2 = 441

Diapositiva 14

Como resultado, se obtiene un nuevo concepto:

Observamos un conjunto de datos y nos fijamos en el valor que se encuentra - en términos generales - en el "centro", de modo que exactamente la mitad de los datos se encuentran por delante y por detrás de este valor. Este valor se denomina mediana.

¿Y si no hay tal "medio" porque tenemos un número par de valores? No hay problema, entonces la mediana es la media aritmética de los dos valores medios.

En el ejemplo, la mediana del interés por las matemáticas es igual a 3 y la mediana del interés por el español es igual a 4. Por lo tanto, también en este caso la asignatura de español va por delante.

Diapositiva 15

¿No es superfluo introducir otro valor medio si, de todas formas, siempre se reduce a lo mismo? Claro, si fuera así. Pero no tiene por qué ser así y eso es lo que deberían mostrar los nuevos datos de la encuesta.

Esta vez se trata de las notas del último examen de 27 alumnos del grupo 8a y 29 alumnos del grupo 8b. Aquí puede ver las cifras absolutas de las notas individuales.

Las notas son algo especial. Se utilizan de forma diferente en todas partes. A veces van del 0 al 10, a veces del 1 al 6, a veces el número pequeño es la mejor calificación, a veces el número grande, a veces incluso se utilizan letras. En el ejemplo, consideramos las notas de 0 a 5, donde 5 es la mejor nota.

Diapositiva 16

Si calculamos la media aritmética y la mediana, la media aritmética de m = 2.7 es la misma en los dos grupos. La mediana, sin embargo, difiere en un grado y es de 2 en 8a y 3 en 8b.

Diapositiva 17

Volvamos a ver esto en el gráfico de barras. Obviamente, hay una distribución de frecuencias muy diferente en los dos grupos. En el grupo 8a los alumnos con las notas realmente malas 1 y 0 apenas están representados, la nota 2 se dio con bastante frecuencia y las mejores notas 5, 4 y 3 se pueden ver, pero también en menor número.

En el grupo 8b hay un pico en las marcas 4 y 3, por lo demás se utiliza toda la gama de marcas. Esto lleva a la diferencia de la mediana con una media aritmética idéntica.

Diapositiva 18

Obviamente, los valores medios no siempre son suficientemente indicativos, pero la dispersión de los datos también es importante. En consecuencia, uno se interesa por la forma en que los valores se desvían de un valor medio. Veamos esta "medida de desviación".

Diapositiva 19

La media aritmética en ambos grupos fue 2.7. Veamos cómo se desvían los distintos valores medidos de esta media aritmética:

Para ello, se forman las diferencias. 5 – 2.7 = 2.3; 4 – 2.7 = 1.3; 3 – 2.7 = 0.3 etc.

Diapositiva 20

Y ahora ponderamos estas diferencias. Calculamos para el grupo 8a

2 • 2,3 + 4 • 1,3 + 6 • 0,3 + 14 • 0,7 + 1 • 1,7 + 0 • 2,7 = 23,1

Diapositiva 21

Para el grupo 8b es

2 • 2,3 + 8 • 1,3 + 8 • 0,3 + 5 • 0,7 + 3 • 1,7 + 3 • 2,7 = 34,1

Diapositiva 22

Se puede calcular la desviación media dividiendo cada una de ellas por el número de estudiantes.

.

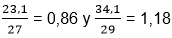Estos sencillos cálculos ya dan una idea de las diferencias. En el grupo 8a, las notas medidas se desvían menos de la media aritmética que en el grupo 8b.

Diapositiva 23

Ese es el principio, pero en la práctica se hace de forma un poco diferente. Se calcula la diferencia entre un único valor y la media aritmética, se eleva al cuadrado este número (no hay más problemas con el signo) y se calcula la suma de todos estos n números. Por último, divide, pero normalmente no por n, sino por n-1. Este número se llama varianza. Y si tomas la raíz de esto, obtienes la desviación estándar.

Así que en el ejemplo partimos de

2,3² = 5,29; 1,3² = 1,69; 0,3² = 0,09; 0,7² = 0,49; 1,7² = 2,89; 2,7² = 7,29.

Diapositiva 24

Ahora ponderamos las diferencias con estos términos cuadráticos primero para el grupo 8a. Dos estudiantes dieron un 5 como nota del examen, por lo que 5,29 con un factor de 2 entra en esta suma. Cuatro estudiantes dieron un 4, por lo que 1,69 con un factor de 4 entra en esta suma. Y así hasta la nota 0, que nadie tuvo en el último examen, por lo que 7,29 se multiplica por 0.

La suma da 27,63, la división entre 26 da 1,063 y la raíz cuadrada es 1,03. Por tanto, el rechazo estándar es Ơ (Sigma) = 1,03.

Para el grupo 8b ocurre lo mismo y obtenemos Ơ (Sigma) = 1,44

Diapositiva 25

Se puede observar que los valores medidos en el grupo 8b son mucho más dispersos que en 8a. Esto también puede explicarse cualitativamente.

Con la desviación estándar Ơ, ahora tenemos una medida fiable para esto:

Un consejo: calcule usted mismo un ejemplo de esto. Así quedará mucho más claro por qué este procedimiento tiene sentido. En particular, puede ver por qué las grandes diferencias con respecto al valor medio son muy importantes y por qué las diferencias más pequeñas tienden a ser despreciadas.

Y sí, ciertamente se podría hacer de otra manera. Este enfoque no es obligatorio; sin duda existen otras medidas de dispersión. Esto permitiría introducir las diferencias de forma diferente, es decir, descuidarlas o enfatizarlas de forma diferente. Esta libertad es sin duda uno de los problemas de la estadística para algunos estudiantes.

Diapositiva 26

Esto es todo por hoy, fue un episodio quizás no muy fácil. Espero que aún se haya divertido un poco. Muchas gracias por estar conmigo. Espero verle la próxima vez.