Diapositiva 0

Bienvenidos y bienvenidas a este nuevo episodio. Hoy queremos recordar algunos materiales escolares que se refieren a la estadística y la probabilidad en un sentido muy amplio. Se trata del teorema del binomio y del triángulo de Pascal.

Diapositiva 1

Empecemos con el teorema del binomio. Ya habíamos hablado de ello porque este teorema es una herramienta útil cuando se consideran situaciones en la estadística y la probabilidad.

¿Qué queremos hoy? Bueno, entenderlo muy bien y conocer mejor algunos aspectos relacionados. ¿Le parece bien? ¿Listo para el nuevo episodio? Entonces, charlemos sobre las matemáticas.

Diapositiva 2

Seguro que se acuerda del teorema del binomio en su forma más sencilla. Se aplica

(a+b)² = a² +2ab + b²  

para todos los números reales a y b.

Se puede calcular de forma muy sencilla:

(a+b)² = (a+b) • (a+b) = a² + ab + ba + b².

Como la ley conmutativa se aplica a la multiplicación de números reales, es

a² + ab + ba + b² = a² +2ab + b².

Es fácil, pero admítalo, también bastante aburrido.

Diapositiva 3

Para la enseñanza en el colegio, también hay métodos que demuestran vivamente su validez. Hay aquí un ejemplo. En un cuadrado de lado a+b, se dibujan un cuadrado de lado a y otro de lado b.

Entonces se crean simultáneamente dos rectángulos con lados a y b. Por supuesto, esto no es una demostración en el sentido clásico, pero hace que el teorema sea muy plausible.

Diapositiva 4

También se pueden representar las fórmulas de (a-b)² y (a+b) • (a-b) de forma similar, pero eso nos distraería del tema aquí. Inténtelo usted mismo.

Diapositiva 5

Dibujar en tres o más dimensiones no es un ejercicio muy sencillo o es imposible. Realmente no es posible para n > 2.

Así que vamos a calcular. Es (a+b)³ = (a+b)² • (a+b) = 1a³ + 3a²b + 3ab² + 1b³ . Los números 1 antes de a³, 3 antes de a²b, 3 antes de ab² y 1 antes de b³ se llaman -seguramente ha oído el término - coeficientes.

Se puede seguir calculando así, y así lo hicimos para (a+b)⁴. Pero la multiplicación se convierte rápidamente en algo muy confuso. Seguir así a mano no sería nada divertido. Como casi siempre, aquí también necesitamos un enfoque sistemático.

Diapositiva 6

Pero casi obviamente, los coeficientes evolucionan uno de otro con cada nueva ecuación.

Veamos el paso de (a+b)² a (a+b)³. Al multiplicar por a, el término a² se convierte en el término a³. El término 2ab se convierte en 2a²b y b² en el término ab².

Diapositiva 7

Al multiplicar por b, el término a² se convierte en el término a²b. El término 2ab se convierte en 2ab² y b² en el término b³.

Si resumimos, a³ y b³ aparecen una vez cada uno y los términos mixtos a²b y ab² aparecen tres veces cada uno.

En principio, esto se puede trasladar a (a+b)⁴. Por supuesto, los términos a⁴ y b⁴ deben aparecer con el coeficiente 1. Y luego están todos los términos mixtos posibles, es decir, a³b, a²b² y ab³. La frecuencia con la que se producen puede leerse en el término escrito para (a+b)³. Simplemente hay que formar la suma de los coeficientes adyacentes, porque determinan el siguiente cálculo. Inténtalo para (a+b)⁵.

Diapositiva 8

Este es el resultado:

(a+b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5a⁴b + b⁵.

Mira esto de nuevo. En realidad, se trata de simple aritmética.

Diapositiva 9

Los coeficientes forman el triángulo de Pascal. Cada coeficiente es la suma de los dos coeficientes anteriores. Y en cada uno de los "bordes" hay un "1".

Diapositiva 10

Aquí puede ver una vez más para (a+b)² y (a+b)³ la conexión entre las ecuaciones y el triángulo de Pascal.

Diapositiva 11

Este triángulo de Pascal también se puede escribir de esta manera, es decir, con la ayuda de los coeficientes binomiales. ¿De qué se trata exactamente?

Diapositiva 12

Lo afirmamos. El término se llama coeficiente binomial. El nombre es apropiado porque está obviamente determinado por los coeficientes del triángulo de Pascal. Se llama (y ya lo sabemos) "n sobre k". Aquí, n es un número natural, k es un número natural o 0 y k ≤ n.

Diapositiva 13

Aquí se puede ver de nuevo de forma bastante explícita dónde se encuentran los coeficientes binomiales en el triángulo de Pascal.

Diapositiva 14

Así lo vimos en el episodio 7 (y recuerda que Mayte quería meter exactamente 5 de sus 12 vestidos en la maleta):

El número de subconjuntos de k elementos de un conjunto de n elementos es

 =: .

En ese momento, llamamos a este número n sobre k - con la misma notación, por supuesto.

Diapositiva 15

Pero recuerde: ya habíamos definido este término en otro lugar. 

¿Está permitido hacerlo dos veces en las matemáticas?

Por supuesto que no. Más bien hay que demostrar que ambos conceptos son idénticos.

Diapositiva 16

La demostración no es difícil, pero sí mucho cálculo.

Por eso no nos lo tomamos demasiado en serio. Con el método probado paso a paso, tratamos de hacer plausible la identidad de los dos.

En el primer paso se observa (a+b)⁰ = 1.

Procedemos aquí como de costumbre y, en consecuencia, no nos molestamos con . Ponemos  := 1.

Diapositiva 17

En el segundo paso, se analiza  y . Se puede calcular según la regla y se obtiene

 =

 =

Diapositiva 18

En el tercer paso, consideramos que  = n y también  = n y se aplica a todos los números naturales n.

Aquí puede ver los cálculos necesarios, que son fáciles de seguir.

Así que también se cumple para el segundo y penúltimo número de la fila del triángulo.

 =

 =

Diapositiva 19

El cuarto paso explica la simetría del coeficiente binomial, que puede ver aquí en la diapositiva. Hay que demostrar que

 =  para todos los números naturales n y k ≥ 0.

Diapositiva 20

Este cálculo también es sencillo de entender.

Diapositiva 21

Los pasos de cálculo son sencillos, pero el contenido puede parecer difícil de aplicar.

E incluso ahí hay conceptos erróneos.

En un estudio realizado por Fischbein y Schnarch en 1997, los participantes tuvieron problemas con esta tarea:

Si un comité debe seleccionar dos miembros entre diez candidatos, entonces hay

• más,
• menos o
• el mismo número

de posibilidades como en el caso de la selección de ocho miembros entre diez candidatos.

En el grado 11, el 15% dio una respuesta correcta, y en un grupo de estudiantes de la universidad, sólo el 6%. La mayoría consideró que había más opciones a la hora de elegir 2 personas de 10 que a la hora de elegir 8 de 10.

Nos hemos tomado muchas molestias para demostrar que no hay diferencia, porque 10 sobre 2 es lo mismo que 10 sobre 8. Pero obviamente no es realmente intuitivo.

Diapositiva 22

El quinto paso es el que más cálculos requiere.

Demostramos que  =  +  para todos los números naturales n y k ≥ 0. Por lo tanto, encaja que dos números adyacentes en el triángulo de Pascal sumen el número que está debajo de ellos.

En la parte derecha de la diapositiva se puede ver esto de nuevo en las líneas correspondientes del triángulo de Pascal.

Diapositiva 23

Entonces se hace el cálculo. En primer lugar, las fracciones se llevan al denominador principal. Básicamente, esto es simple. Pero como los factores individuales son productos como (n-k-1)! esto se vuelve un poco difícil de manejar. Léalo usted mismo, o confíe en mi palabra, aunque no debería hacerlo en matemáticas.

Diapositiva 24

Se suma. Esto tampoco es difícil, pero rápidamente se vuelve confuso.

Diapositiva 25

Por tanto, podemos utilizar el coeficiente binomial para formular el teorema del binomio.

Lo siguiente se aplica a todos los números reales a, b y a todos los números naturales n:

 

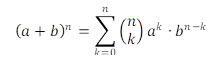Diapositiva 26

Bueno, y también se podría escribir así. Esto es la simetría.

 

 

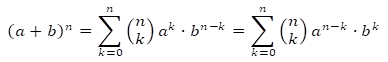
Diapositiva 27

Eso fue todo por hoy. Muchas gracias por acompañarme en esta charla matemática. Hasta la próxima.